Snow falls in winter and melts in spring, but what drives the phase change in between?
Although melting is a familiar phenomenon encountered in everyday life, playing a part in many industrial and commercial processes, much remains to be discovered about this transformation at a fundamental level.
In 2015, a team led by the University of Michigan’s Sharon Glotzer used high-performance computing at the Department of Energy’s (DOE’s) Oak Ridge National Laboratory to study melting in two-dimensional (2-D) systems, a problem that could yield insights into surface interactions in materials important to technologies like solar panels, as well as into the mechanism behind three-dimensional melting. The team explored how particle shape affects the physics of a solid-to-fluid melting transition in two dimensions.
Using the Cray XK7 Titan supercomputer at the Oak Ridge Leadership Computing Facility (OLCF), a DOE Office of Science User Facility, the team’s work revealed that the shape and symmetry of particles can dramatically affect the melting process. This fundamental finding could help guide researchers in search of nanoparticles with desirable properties for energy applications.
To tackle the problem, Glotzer’s team needed a supercomputer capable of simulating systems of up to 1 million hard polygons, simple particles used as stand-ins for atoms, ranging from triangles to 14-sided shapes. Unlike traditional molecular dynamics simulations that attempt to mimic nature, hard polygon simulations give researchers a pared-down environment in which to evaluate shape-influenced physics.
“Within our simulated 2-D environment, we found that the melting transition follows one of three different scenarios depending on the shape of the systems’ polygons,” University of Michigan research scientist Joshua Anderson said. “Notably, we found that systems made up of hexagons perfectly follow a well-known theory for 2-D melting, something that hasn’t been described until now.”
Shifting Shape Scenarios
In 3-D systems such as a thinning icicle, melting takes the form of a first-order phase transition. This means that collections of molecules within these systems exist in either solid or liquid form with no in-between in the presence of latent heat, the energy that fuels a solid-to-fluid phase change . In 2-D systems, such as thin-film materials used in batteries and other technologies, melting can be more complex, sometimes exhibiting an intermediate phase known as the hexatic phase.
The hexatic phase, a state characterized as a halfway point between an ordered solid and a disordered liquid, was first theorized in the 1970s by researchers John Kosterlitz, David Thouless, Burt Halperin, David Nelson, and Peter Young. The phase is a principle feature of the KTHNY theory, a 2-D melting theory posited by the researchers (and named based on the first letters of their last names). In 2016 Kosterlitz and Thouless were awarded the Nobel Prize in Physics, along with physicist Duncan Haldane, for their contributions to 2-D materials research.
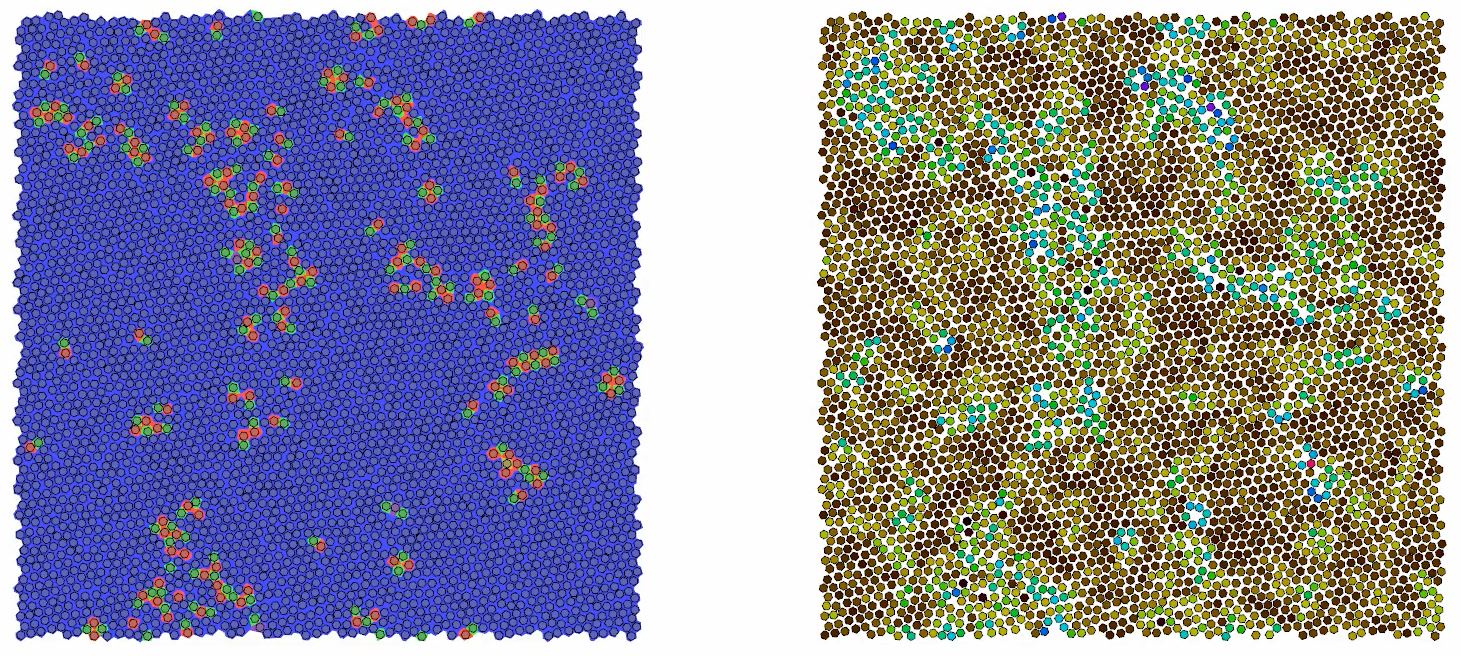
At the molecular level, solid, hexatic, and liquid systems are defined by the arrangement of their atoms. In a crystalline solid, two types of order are present: translational and orientational. Translational order describes the well-defined paths between atoms over distances, like blocks in a carefully constructed Jenga tower. Orientational order describes the relational and clustered order shared between atoms and groups of atoms over distances. Think of that same Jenga tower turned askew after several rounds of play. The general shape of the tower remains, but its order is now fragmented.
The hexatic phase has no translational order but possesses orientational order. (A liquid has neither translational nor orientational order but exhibits short-range order, meaning any atom will have some average number of neighbors nearby but with no predicable order.)
Deducing the presence of a hexatic phase requires a leadership-class computer that can calculate large hard-particle systems. Glotzer’s team gained access to the OLCF’s 27-petaflop Titan through the Innovative and Novel Computational Impact on Theory and Experiment (INCITE) program, running its GPU-accelerated HOOMD-blue code to maximize time on the machine.
On Titan, HOOMD-blue used 64 GPUs for each massively parallel Monte Carlo simulation of up to 1 million particles. Researchers explored 11 different shape systems, applying an external pressure to push the particles together. Each system was simulated at 21 different densities, with the lowest densities representing a fluid state and the highest densities a solid state.
The simulations demonstrated multiple melting scenarios hinging on the polygons’ shape. Systems with polygons of seven sides or more closely followed the melting behavior of hard disks, or circles, exhibiting a continuous phase transition from the solid to the hexatic phase and a first-order phase transition from the hexatic to the liquid phase. A continuous phase transition means a constantly changing area in response to a changing external pressure. A first-order phase transition is characterized by a discontinuity in which the volume jumps across the phase transition in response to the changing external pressure. The team found pentagons and fourfold pentilles, irregular pentagons with two different edge lengths, exhibit a first-order solid-to-liquid phase transition.
The most significant finding, however, emerged from hexagon systems, which perfectly followed the phase transition described by the KTHNY theory. In this scenario, the particles’ shift from solid to hexatic and hexatic to fluid in a perfect continuous phase transition pattern.
“It was actually sort of surprising that no one else has found that until now,” Anderson said, “because it seems natural that the hexagon, with its six sides, and the honeycomb-like hexagonal arrangement would be a perfect match for this theory” in which the hexatic phase generally contains sixfold orientational order.
Glotzer’s team, which recently received a 2017 INCITE allocation, is now applying its leadership-class computing prowess to tackle phase transitions in 3-D. The team is focusing on how fluid particles crystallize into complex colloids—mixtures in which particles are suspended throughout another substance. Common examples of colloids include milk, paper, fog, and stained glass.
“We’re planning on using Titan to study how complexity can arise from these simple interactions, and to do that we’re actually going to look at how the crystals grow and study the kinetics of how that happens,” said Anderson.
Related Publication: Joshua A. Anderson, James Antonaglia, Jaime A Millan, Michael Engel, and Sharon C. Glotzer, “Fluid-to-Solid Transition of Hard Regular Polygons,” Preprint: arXiv:1606.00687.
Oak Ridge National Laboratory is supported by the US Department of Energy’s Office of Science. The single largest supporter of basic research in the physical sciences in the United States, the Office of Science is working to address some of the most pressing challenges of our time. For more information, please visit science.energy.gov.