Researchers combining the supercomputing muscle of Oak Ridge National Laboratory’s (ORNL’s) Jaguar with the experimental abilities of powerful research magnets have confirmed an exotic quantum state known as Bose glass.
In it, particles condense into separate regions within a material, with the particles in each region sharing the same wave function. This is the closest that particles in a quantum mechanical system can get to being in the same place at the same time.
The researchers, affiliated with institutions spread across three continents, published their findings in the September 2012 issue of the journal Nature.
Bose glass is a form of condensed matter related to superfluids (liquids with zero viscosity that can, among other things, climb out of their containers) and superconductors (materials that conduct electricity with no resistance). And, like superfluids, and superconductors, Bose glass is found only in very, very cold environments.
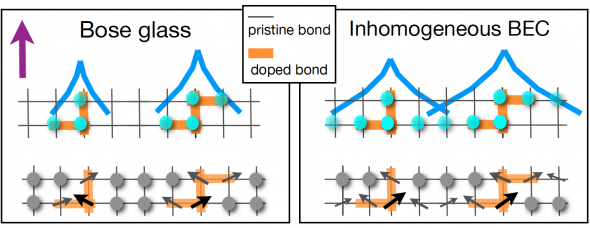
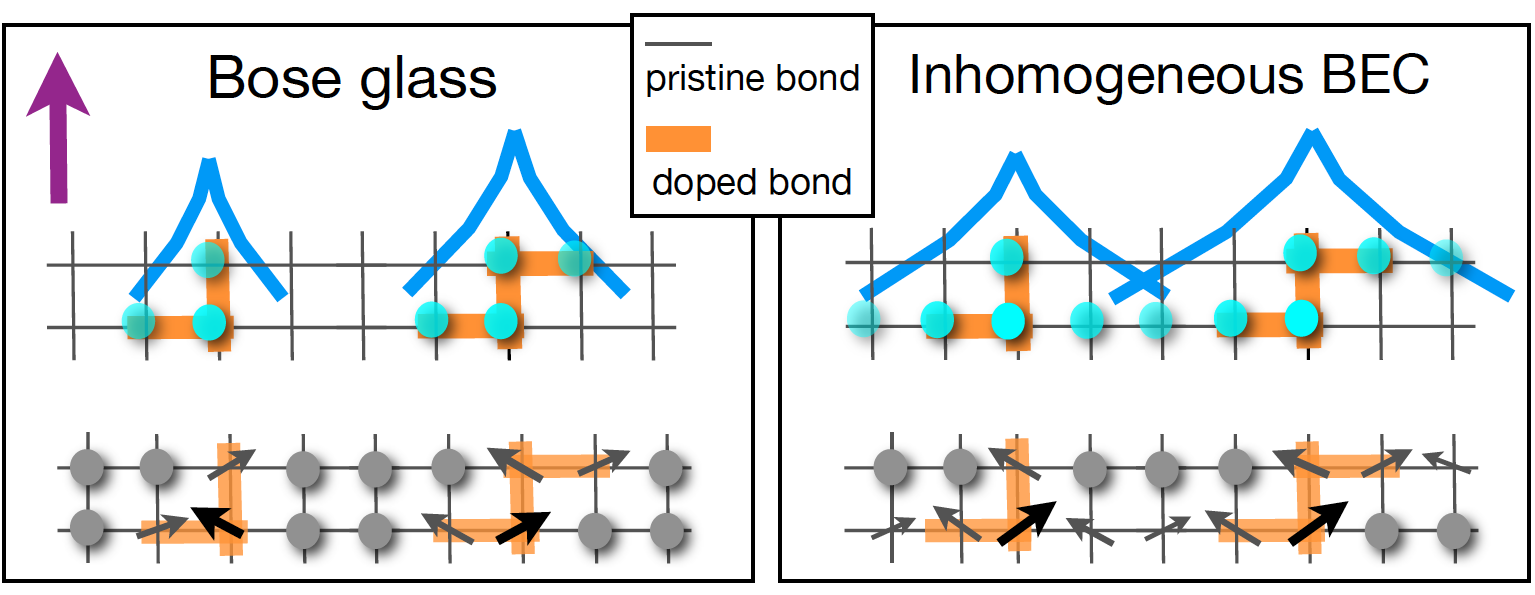
Sketch of Bose glass and inhomogeneous Bose-Einstein condensate. The transition between these two phases is induced by an applied magnetic field (indicated by the violet arrow in the left panel). The upper lines show the phases in terms of quasiparticles (the cyan dots); the lower level in terms of spins (arrows corresponding to atomic magnetic moments). Grey dots symbolize spins that remain unaffected by the applied field. Illustrations courtesy of Tommaso Roscilde, École Normale Supérieure de Lyon
In this collaboration, the calculations performed on Jaguar were able to guide experimental researchers both in creating Bose glass and in confirming that their creation was indeed Bose glass. The computational work was led by Tommaso Roscilde of France’s École Normale Supérieure de Lyon, who worked with colleagues Rong Yu of Rice University and Stephan Haas of the University of Southern California.
“If the theoretical and the experimental data match up for the macroscopic properties, one gains from the theoretical study the fundamental information on the microscopic physics at the basis of the observed behavior,” Roscilde said.
A very cold magnet
They focused their exploration on a magnet placed in a powerful magnetic field at a temperature very near absolute zero. The project is concerned not just with the magnet as a whole, but with the magnetic moment of each atom, which can be thought of as a small compass.
Under the influence of the external magnetic field, these atomic moments are partly aligned along the field. The projections of the atomic moments along the field then behave as if they were separate particles, called “quasiparticles.” It is these quasiparticles that condense into a single quantum state.
The condensate relies on several aspects of quantum mechanical systems that may seem very odd.
Quantum oddities
The first is “superposition,” in which a particle can be partly in two contradictory states at the same time. They are not in between the two states; they are in both at the same time. It is as though you could be sitting in two chairs at the same time—not in between, mind you, but with a portion of you solidly in each.
The second oddity depends on the difference between two types of particles: fermions and bosons.
We and the world around us are made of fermions, which include quarks and electrons (everything you need to build an atom). The Pauli exclusion principle says that two fermions cannot occupy the same state, and fermions obey.
This is roughly analogous to saying you cannot sit in a chair that is already occupied—“roughly,” because quantum particles are described by wave functions rather than by classical concepts such as position and velocity. Quantum particles also have quantum spin, with fermions having half-integer spins (1/2, 3/2, etc.).
If particles have integer spins (1, 2, etc.), then they are bosons, and bosons don’t obey the Pauli exclusion principle, meaning they do gather in the same state.
The most famous bosons are the photon, which, among other things, carries light, and the Higgs boson, which may have been uncovered recently at Europe’s Large Hadron Collider and plays a key role in giving objects mass.
Sort of like a particle
Quasiparticles are aspects of a system that behave as though they were particles. They are not uncommon in our everyday lives. A bubble in a carbonated liquid, for instance, is a quasiparticle; it behaves as though it were a separate particle but is really just carbon dioxide displacing the liquid. In our quantum magnet, which is made up of a material called nickel-tetrakis-thiourea, these magnetic quasiparticles have a spin of 0 and therefore share all the strange attributes of a boson, including the ability to gather into a single quantum state.
If the magnet is made of a single material, the quasiparticles gather in a condensate spread across the entire magnet rather than in separate regions. This is Bose-Einstein condensation, so called because Albert Einstein first predicted it based on the work of Indian physicist Satyendra Nath Bose.
To get the quasiparticles to condense into separate areas within the magnet, rather than across the magnet as a whole, the researchers carefully added impurities to the magnet in a process called “doping.”
Doping restricts quasiparticle condensates to specific areas because of the third quantum oddity, which because it is a quantum mechanical system, the particles—or in this case the quasiparticles—behave like waves as well as particles. As a result, the impurities in the magnet are far more important than they would be in a classical system.
A similar modification of a classical system might not be much of a hindrance to motion, since classical particles would be able to flow around the impurities. In a quantum system, however, just as a rock poking out of a pond scatters a wave in the water, an impurity in the magnetic material will scatter the waves of the quasiparticles, partly transmitting them and partly reflecting them.
These transmitted and reflected waves interfere with one another, with the result being that separate condensates gather in areas of the lattice that are relatively free of impurities. While particles will be in the same state as nearby particles, they will not be in the same state as the other islands of condensate.
While Bose-Einstein condensate had been verified experimentally, this is the first experimental confirmation of Bose glass.
“What I find extremely striking,” Roscilde noted, “is that the material in question—doped DTN—is an insulator, and in zero field it does not show any ‘magnetic action’ at all. It is almost completely featureless, one would say. Yet, when you look at it through the eye of quasiparticles, it is a close-to-ideal realization of a model that people in condensed matter physics have worked on for about 25 years—namely interacting bosons in a random environment.
“In this sense, spins can be used here to ‘simulate’ bosons—a bit like your computer can simulate reality, but using quantum units like spins. Given that our understanding of the physics of bosons in a random environment is still incomplete, this quantum simulator might turn out to be very useful for fundamental physics.”
The observation of a Bose glass is currently being pursued in other experimental setups, such as ultracold atoms or liquid helium, but doped DTN is the first to provide such a clear realization of this phase in comparison with the expected theoretical behavior. This shows that quantum magnets are strong candidates for the quantum simulation of interacting bosons.
Monte Carlo computations
The project was a clear example of collaboration between computational and experimental research. In this case the computations came first, with the computational team calculating both the conditions under which Bose glass could be found and the measurements that would confirm it.
Roscilde and his computational colleagues were able to guide the experiments by investigating theoretical models for the material and predicting the circumstances under which the Bose glass phase should be seen.
The team used a Quantum Monte Carlo technique with Jaguar to predict the proper doping of the material for a Bose glass as well as the ideal temperatures and magnetic field for producing the phase.
Monte Carlo methods are a valuable approach to analyzing complex systems. The program generates random values for different conditions and observes how they behave. In this way, the researchers approach the details of a system that cannot be calculated directly.
The simulations averaged around 1,000 bosonic quasiparticles, with inputs such as temperature, magnetic field, and concentration disorder. For each system size, the simulation typically looked at 20 or so applied magnetic field values.
They also predicted the identifying features, or signatures, that demonstrated that the experiment was able to achieve a Bose glass. The computer simulation calculated all aspects of the system that can be measured in an experiment, such as magnetization along the applied field and the specific heat of the system.
Moving forward, Roscilde and his teammates—both computational and experimental—will be exploring this system in more depth.
“We are planning to study the dynamics of the system,” he noted, “namely the nature of the elementary excitations in the Bose glass and the way that such elementary excitations would show up in a neutron scattering experiment.”