Award-winning application analyzes promising materials
Something odd happens when you expose the element gadolinium to a strong magnetic field: Its temperature jumps up. Remove the field and the temperature drops below the starting point.
It’s easy enough to see how this odd behavior, known as the magnetocaloric effect, might prove useful, especially in refrigerators and air conditioners. Instead of having to rely on motorized compressors and other equipment to heat and cool a special refrigerant, they would achieve the same result simply by running gadolinium or some other magnetocaloric material through a magnetic field.
The equipment could get cheaper and more energy efficient. It would almost certainly be simpler and more environmentally benign, releasing us from our dependence on ozone-depleting refrigerants. But there’s a catch, the same one we face in exploiting any potentially useful oddity of physics: We must find—or create—materials that do their magic under the right conditions. So far, we’re not there.
Supercomputer simulation will certainly play a part in getting us there. A team led by Oak Ridge National Laboratory’s (ORNL’s) Markus Eisenbach is making progress in a very important part of this problem. Using an application that took the 2009 Gordon Bell Prize as the world’s most advanced scientific computing application, the team has been simulating the magnetic properties of promising materials, focusing in particular on the magnetocaloric effect. Its work is detailed in three recent papers in the Journal of Applied Physics.
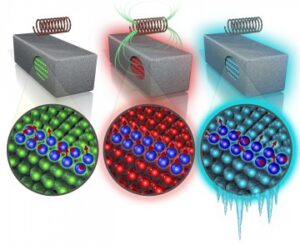
The magnetic moments of atoms in materials used in magnetic refrigeration are naturally disordered (left). When the material is exposed to a magnetic field, the moments align with the field and its temperature rises (center). If the excess heat is removed, the material’s temperature drops below the original point once the magnetic field is withdrawn.—Image by Andy Sproles, ORNL
Every atom has its moment
The magnetocaloric effect is usually found in ferromagnets, materials that lose their magnetism above a certain temperature, known as the Curie temperature. Each atom still has a magnetic strength and direction, known as its magnetic moment, but these moments are pointed every which way. If the material is exposed to a strong enough magnetic field, however, these small, separate magnets partially align in the same direction, making the material as a whole magnetic once more. At the same time the reduction of the magnetic disorder causes the thermal energy associated with the motion of the atoms to rise, making it hotter.
When the magnetic field is withdrawn, the atomic magnets once again point randomly. At this point the energy that had gone into heating the material instead acts to unalign the magnetic moments of the individual atoms, meaning the temperature of the material once again drops. The rising and falling temperatures make these materials natural elements for refrigerators, as long as excess heat can be disposed of.
“Magnetic refrigeration is analogous to the normal refrigeration cycle, where you apply pressure to compress the coolant and then you release the latent heat and evaporate it again and go through the cycle,” Eisenbach noted. “But you have many moving parts, many inefficiencies.
“With the magnetocaloric effect [or MCE], you essentially just move a piece of MCE material, say on a disk, through a magnetic field. You have many fewer moving parts, and it might also be more energy efficient.”
The technique has been used to chill scientific experiments within a hair’s breadth of absolute zero, but it is not yet ready to replace the compressors in your refrigerator and air conditioner.
There are at least three substantial challenges to using the magnetocaloric effect in any widespread commercial application. First, a candidate material must show a large enough shift in temperature as it moves in and out of the magnetic field. Second, it must show that effect near the temperature at which you want to keep a refrigerator or the chilled air being pumped out of an air conditioner.
Third, the material must be readily available. The most promising materials so far—including gadolinium—are rare earth metals found primarily in China. As a result, their availability for future applications in the United States is in question.
In other words, the ideal material has not been found. That’s where Eisenbach’s team and its application, WL-LSMS comes in. The application is able to calculate the magnetic properties of promising materials, including its Curie temperature, from basic laws of physics rather than from models that must incorporate approximations. Because of this approach, it is able to get very close to a material’s actual Curie temperature.
In the Journal of Applied Physics articles, published in April 2011, the team reviewed its experience calculating the properties of three materials: iron, cementite, and an alloy of nickel, manganese, and gallium. It simulated the magnetic properties of iron, which has a Curie temperature of 1,050 K (1,430°F) in two configurations: one with 16 atoms and the other with 250. The 16-atom simulation came up with a Curie temperature of 670 K (746°F). The 250-atom simulation was far more computationally demanding, but also more accurate, coming up with a Curie temperature of 980 K (1,304°F).
The results are very promising, especially in light of earlier attempts to calculate Curie temperatures.
“So, we’re within the accuracy of the approximations we employ,” said Eisenbach. “This is very good. Some other theories predict transition temperatures that are 10 times or so too high.”
For cementite, a material with three parts iron and one part carbon, WL-LSMS got even closer, using a 128-atom simulation to come up with 425 K (305°F), compared to an experimental result of 480 K (404°F).
Finally, the team looked at a more complex and challenging alloy, Ni2MnGa—consisting of two parts nickel combined with one part each of manganese and gallium—that holds promise for magnetic refrigeration. Looking at a 144-atom group, WL-LSMS came up with a Curie temperature of 185 K (–127°F), compared to the observed value of 351 K (172°F).
WL-LSMS combines two methods to achieve its goal. The first—known as locally self-consistent multiple scattering (LSMS)—applies density functional theory to solve the Dirac equation, a relativistic wave equation for electron behavior. The code has a robust history, having been the first code to run at a sustained trillion calculations per second—also known as a teraflop. It earned its developers the Gordon Bell Prize in 1998.
Warming it up
LSMS, though, describes a system in its ground state at a temperature of absolute zero, or nearly –460°F. Eisenbach and colleagues are able to apply this technique to more common temperatures through a Monte Carlo method known as Wang-Landau (WL). In essence, the method forces the atoms to point magnetically in random directions and allows the application to calculate the system’s magnetic and thermal properties.
Each configuration chosen by Wang-Landau will have an energy level. The more configurations found at a given energy level (that is, the higher the density of states), the more chaotic and, therefore, hotter it is.
“Every state has a different energy,” Eisenbach noted. “Now you want to know for each energy how many states are there that have that energy. Once you know this, you can very easily calculate the behavior of the system at different temperatures. You correlate the density of states with the temperature. It’s a simple calculation.”
The tougher calculation, he said, is going through the different states, because each atom can be pointing in essentially an infinite number of possible directions. This is where a Monte Carlo method is needed because it can choose a representative sampling of states.
“There are a gazillion states. You have 250 atoms and each can be pointed in an infinite number of directions. The direction an atom can point to is described by two numbers, and you have 250 atoms. It’s a 500-dimensional integral. And no one can evaluate a 250-dimensional integral directly numerically. So we used this Monte Carlo method.”
The size of the calculations means that the team needs a leadership-class supercomputer such as ORNL’s Jaguar, the most powerful in the country. Eisenbach and colleagues ran WL-LSMS on more than 223,000 of Jaguar’s 224,000-plus available processing cores to reach 1.84 thousand trillion calculations per second (or 1.84 petaflops) and win the Gordon Bell Prize in 2009. The team’s recent calculations have been similarly massive.
Eisenbach noted that these calculations are important for more than just magnetic refrigeration. For example, they can help researchers understand the properties of different types of steel, a pursuit whose payoff may be the creation of lighter, stronger, and more reliable materials (for example, within a nuclear reactor containment vessel). In this case, he said, the magnetic properties of steel are part of a much larger exploration well beyond the capabilities of current supercomputers. Such a problem will likely require exascale supercomputers capable of millions of trillions of calculations each second.
“The ultimate goal is to be able to look at what’s the thermal behavior around a defect. You not only produce damage, but it also happens at finite temperature. You want to be able to really get a better picture of how the material behaves,” Eisenbach explained.
“It’s essentially not even putting the puzzle together, but finding the puzzle pieces. For a holistic picture we’re probably talking about an exascale problem.”
Related Publications:
First principles approach to the magneto caloric effect: Application toNi2MnGa
D. M. Nicholson, Kh. Odbadrakh, A. Rusanu, M. Eisenbach, G. Brown, and B. M. Evans, III
J. Appl. Phys. 109, 07A942 (2011)
Calculated electronic and magnetic structure of screw dislocations in alpha iron
K. Odbadrakh, A. Rusanu, G. M. Stocks, G. D. Samolyuk, M. Eisenbach, Yang Wang, and D. M. Nicholson
J. Appl. Phys. 109, 07E159 (2011)
Improved methods for calculating thermodynamic properties of magnetic systems using Wang-Landau density of states
G. Brown, A. Rusanu, M. Daene, D. M. Nicholson, M. Eisenbach, and J. Fidler
J. Appl. Phys. 109, 07E161 (2011)






